平面上で原点を極、
軸の正の部分を始線とする極座標に関して、極方程式
\begin{equation}
r = 2 +\cos \theta \quad (0 \leqq \theta \leqq \pi)
\end{equation}により表される曲線をとする。
解答例
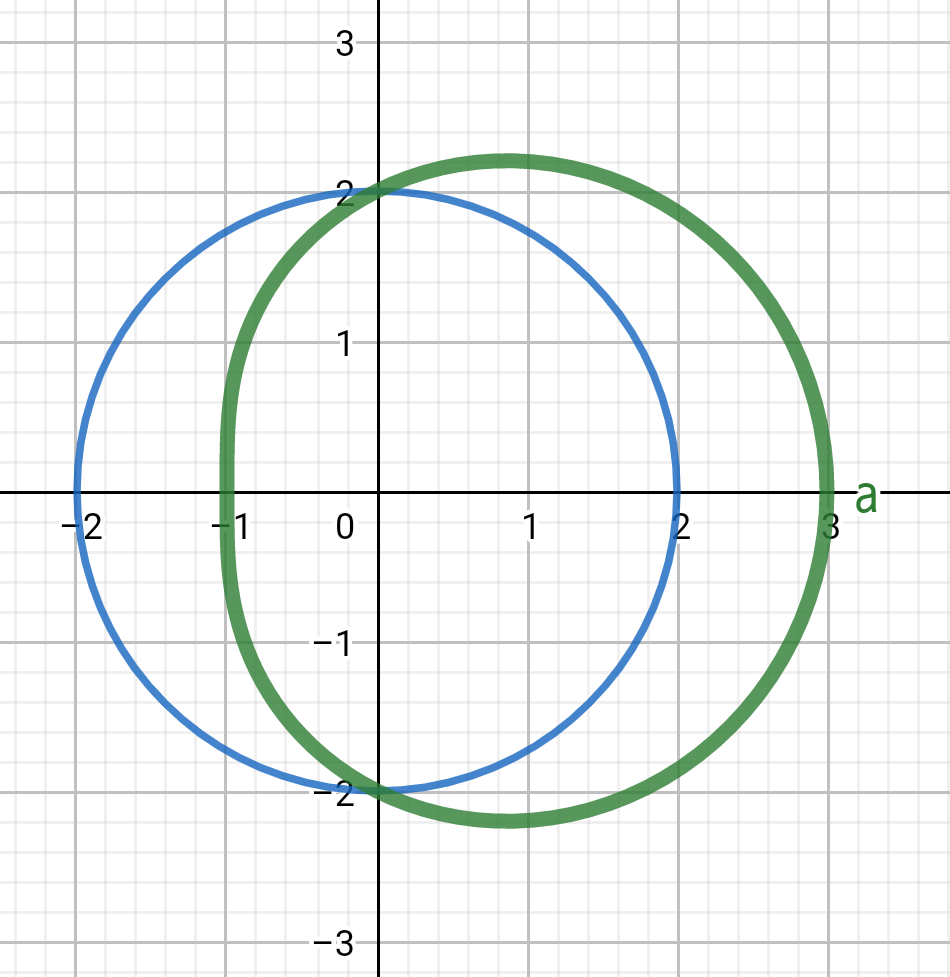
曲線と
軸の交点は(3, 0), (-1, 0)なので、立体の体積は
\begin{equation}
V = \pi \int_{-1}^3 y^2 \, dx
\end{equation}です。
\begin{equation}
x^2 +y^2 = r^2
\end{equation}なので
\begin{equation}
V = \pi \int_{-1}^3 (-x^2 +r^2) \, dx \tag{1}
\end{equation}となります。
式(1)の括弧内の第1項は
\begin{eqnarray}
\int_{-1}^3 x^2 \, dx &=& \left[ \ \frac{1}{3} \, x^3 \ \right]_{-1}^3 \\
&=& 9 +\frac{1}{3} = \frac{28}{3} \tag{2}
\end{eqnarray}です。
第2項について、
\begin{eqnarray}
x &=& r \cos \theta \\
&=& 2\cos \theta +\cos^2 \theta \\
\\
dx &=& -2\sin \theta -2\cos \theta \sin \theta \\
&=& -2(1 +\cos \theta) \sin \theta
\end{eqnarray} \begin{array}{|c|ccc|}
\hline
x & -1 & \to & 3 \\ \hline
\theta & \pi & \to & 0 \\ \hline
\end{array}なので、
\begin{eqnarray}
\int_{-1}^3 r^2 \, dx &=& \int_\pi^0 (4 +4\cos \theta +\cos^2 \theta)(-2)(1 +\cos \theta) \sin \theta \, d\theta \\
&=& 2\int_0^\pi (4 +4\cos \theta +\cos^2 \theta)(1 +\cos \theta) \sin \theta \, d\theta
\end{eqnarray}となります。
定積分の置換積分 - 数式で独楽する
さらに、
\begin{equation}
\cos \theta = t
\end{equation}とすると、
\begin{equation}
-\sin \theta \, d\theta = dt
\end{equation} \begin{array}{|c|ccc|}
\hline
\theta & 0 & \to & \pi \\ \hline
t & 1 & \to & -1 \\ \hline
\end{array}なので、
\begin{eqnarray}
\int_{-1}^3 r^2 \, dx &=& 2\int_{-1}^1 (4 +4t +t^2)(1 +t) \, dt \\
&=& 2 \left[ \frac{1}{3} \, (t +2)^3 (t +1) \right]_{-1}^1 -\frac{2}{3} \int_{-1}^1
(t +2)^3 \, dt \\
&=& 2 \cdot \frac{1}{3} \cdot 27 \cdot 2 -\frac{2}{3} \left[ \frac{1}{4} \, (t +2)^4 \right]_{-1}^1 \\
&=& 36 -\frac{2}{3} \cdot \frac{1}{4} \, (81 -1) \\
&=& 36 -\frac{40}{3} \\
&=& \frac{68}{3} \tag{3}
\end{eqnarray}となります。
定積分の置換積分 - 数式で独楽する
式(1), (2), (3)より、求める体積は
\begin{equation}
V = \pi \left( -\frac{28}{3} +\frac{68}{3} \right) = \frac{40}{3} \, \pi
\end{equation}となります。
