円周角の定理

円周角の定理

1. 同一の円弧に対する円周角は中心角の半分に等しい
2. 同一の円弧に対する円周角は等しい

「中心角」は、円弧の両端をそれぞれ中心と結んだときに中心にできる角をいいます。
「円周角」は、円弧の両端をそれぞれ当該円弧上にない円周上の点と結んだときに円周上にできる角をいいます。

「円周角は中心角の半分」の証明

さて、証明ですが、命題の文章を見ても手掛かりがなく、途方に暮れてしまいます。

取り敢えず、中心角と円周角の位置関係を分類すると、次のようになります。

1. 中心角をなす直線の一方が円周角をなす直線と一致する場合
2. 中心角が円周角の内部にある場合
3. 中心角が円周角の外部にある場合

場合分けに漏れや重複(ダブり)がないことを確認してください。

特殊な形をまず攻めることで、普遍的な形への足掛かりとしていくことになります。

点Oを中心とする円の弧をAB、弧AB上にない円周上の点をPとし、円周角APBと中心角AOBの関係を見ていきます。

(1) 中心角をなす直線の一方が円周角をなす直線と一致する場合

三角形OBPに着目します。

辺OB, OPは円の半径なのでOB=OPです。よって、三角形OBPは二等分三角形です。したがって、

∠OPB = ∠OBP
です。

角AOBは角POBの外角なので、

∠AOB =∠OPB + ∠OBP
です。

したがって、

∠AOB = 2 ∠APB
すなわち、円周角は中心角の半分の大きさとなります。

(2) 中心角が円周角の内部にある場合

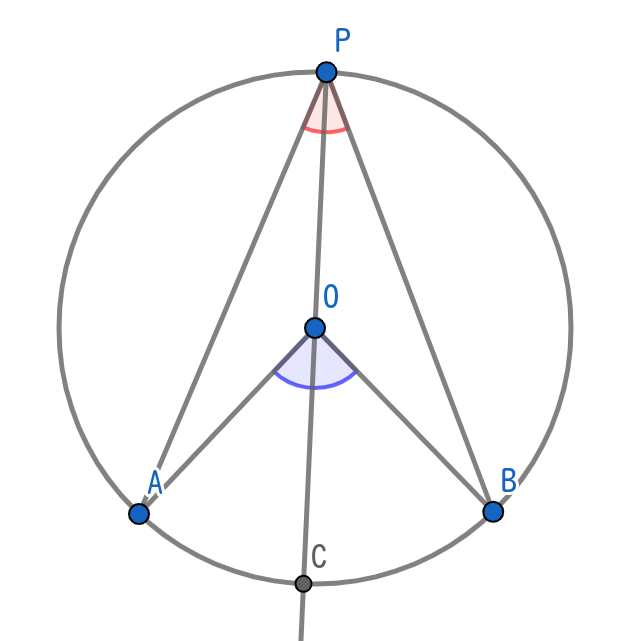
補助線POを引き、弧ABとの交点をCとします。
すると、弧CAとCBについて、それぞれ上記(1)に帰着できることが分かります。
つまり、

∠COA = 2 ∠CPA
∠COB = 2 ∠CPB
が成り立ちます。
一方、
∠AOB = ∠COA + ∠COB
∠APB = ∠CPA + ∠CPB
なので、
∠AOB = 2 ∠OPB
となります。
この場合も、円周角は中心角の半分の大きさとなります。

(3) 中心角が円周角の外部にある場合

補助線POを引き、弧ABとの交点をCとします。
すると、弧CAとCBについて、それぞれ上記(1)に帰着できることが分かります。
つまり、

∠COA = 2 ∠CPA
∠COB = 2 ∠CPB
が成り立ちます。
一方、
∠AOB = ∠COA - ∠COB
∠APB = ∠CPA - ∠CPB
なので、
∠AOB = 2 ∠OPB
となります。
この場合も、円周角は中心角の半分の大きさとなります。

(1)~(3)のまとめ

上記(1)~(3)により、いずれの場合においても、

円周角は中心角の半分の大きさ
となります。

「円周角は等しい」の証明

前項で「同一の円弧に対する円周角は中心角の半分に等しい」ことを証明しました。
したがって、

同一の円弧に対する円周角は等しい
ことを導くことができます。