ロルの定理

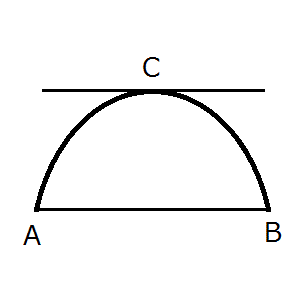
ロル(Rolle)の定理
関数が区間で連続、区間で微分可能であり、
\begin{equation}
f(a)=f(b)
\end{equation}である場合、
\begin{equation}
f'(c) = 0
\end{equation}を満たすが存在する。

ロルの定理は、平均値の定理やテイラーの定理などを導く重要な定理です。
しかし、それ以外の使い途がない、少し寂しい定理でもあります。

では、証明にいきます。

関数が定数関数である場合

任意ので、
\begin{equation}
f'(x)=0
\end{equation}です。定数の微分は0なので、当然です。

関数に、となるが存在する場合

が最大となるが存在します。
なので、当然ですね。
このとき、を証明します。

関数が、

• で微分可能である
• である

ことから、
\begin{eqnarray}
f'(c) &=& \lim_{h \to +0} \frac{f(c+h) - f(c)}{h} & \leq & 0 \\
f'(c) &=& \lim_{h \to -0} \frac{f(c+h) - f(c)}{h} & \geq & 0
\end{eqnarray}
が成り立ちます。*1

したがって、
\begin{equation}
f'(c) = 0
\end{equation}となります。

関数に、となるが存在する場合

先ほどと同様にして、
\begin{equation}
f''(c) = 0
\end{equation}が得られます。
正負が先ほどと逆になるだけで、あとは同じです。

まとめ

以上のことから、
関数が区間で連続、区間で微分可能であり、
\begin{equation}
f(a)=f(b)
\end{equation}である場合、
\begin{equation}
f'(c) = 0
\end{equation}を満たすが存在する
ことが証明されます。

*1:分子は負、分母は上の式では正で下の式では負です。