円錐を平面で切断すると、
- 円
- 楕円
- 放物線
- 双曲線
が得られます。これらを総称して、円錐曲線と呼ばれます。
2つの合同な円錐を頂点で向かい合わせた状態で、片方の円錐を通過する平面で切断すると、断面は楕円になります。
具体的を示します。
\begin{equation}
x^2 + y^2 =z^2 \tag{1}
\end{equation}で表される円錐を、軸を中心に
回転させます。
とします。つまり、式(1)において、
\begin{eqnarray}
x & \to & x \cos \theta -z \sin \theta \\
z & \to & x \sin \theta +z \cos \theta
\end{eqnarray}と置き換えます。
回転行列 - 数式で独楽する
変形します。
\begin{eqnarray}
(x \cos \theta -z \sin \theta)^2 +y^2 &=& (x \sin \theta +z \cos \theta)^2 \\
x^2 (\cos^2 \theta -\sin^2 \theta) -4xz \cos \theta \, \sin \theta +y^2 &=& z^2 (\cos^2 \theta -\sin^2 \theta)
\end{eqnarray}倍角の公式を用い、
\begin{equation}
x \cos 2\theta -2xz \sin 2\theta +y^2 = z^2 \cos 2\theta \tag{2}
\end{equation}を得ます。
倍角の公式 - 数式で独楽する
の場合、式(2)の両辺を
で割ることができ、
\begin{equation}
x^2 -2xz \tan 2\theta +\frac{y^2}{\cos 2\theta} = z^2
\end{equation}となります。もう少し整理して
\begin{equation}
(x -z \tan 2\theta)^2 +\frac{y^2}{\cos 2\theta} = z^2 (1 +\tan^2 2\theta) \tag{3}
\end{equation}を得ます。
の場合、
なので、式(3)は楕円となります。
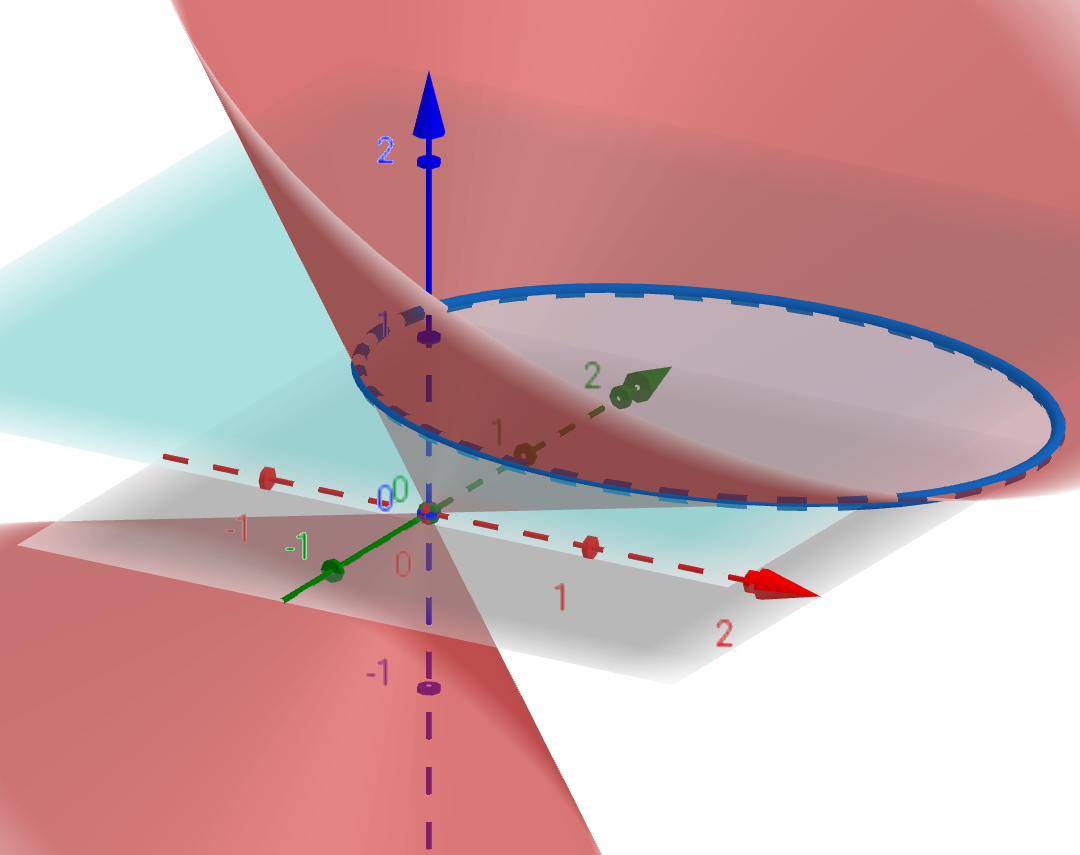
例えばとすると、式(3)は
\begin{equation}
\left( x -\sqrt{3}\, z \right)^2 +y^2 = 4z^2
\end{equation}となります。
なら正円です。
を増やしていくと、楕円は長軸方向に引き伸ばされていきます。
の場合はこちら
(リンク)
の場合はこちら
円錐曲線その3~放物線 - 数式で独楽する