円周角の定理の逆

円周角の定理とは、

1. 同一の円弧に対する円周角は中心角の半分に等しい
2. 同一の円弧に対する円周角は等しい

円周角の定理 - 数式で独楽する
ということですが、2項を図に描いて表すと次のようになります。

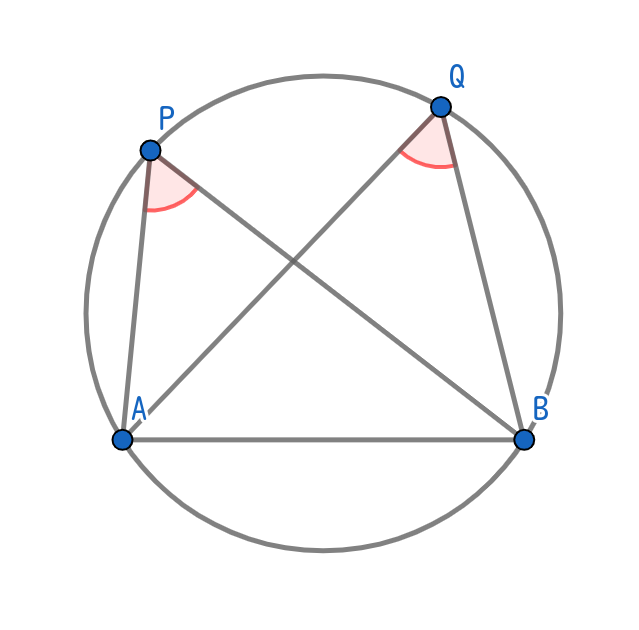
円周上に4点A, B, P, Qがあり、P, Qは弦ABに対し同じ側にあるとき、

∠APB = ∠AQB
が成り立つ。

これに対し、「円周角の定理の逆」とは、次の命題をいいます。

「円周角の定理の逆」
線分ABの同じ側にある2点P, Qが

∠APB = ∠AQB
を満たすならば、
4点A, B, P, Qは同一円周上に存在する。

3点A, B, Pを通る円は一意に定まるので、点Qがこの円周上に存在することを示すことになります。

3点A, B, Pを通る円を$O$とし、$O$上に点Q'を定めます。ただし、点Q'は弦ABに対し点Pと同じ側にあるものとします。
円周角の定理により、

∠AQ'B = ∠APB
となります。

∠AQB < ∠APBの場合

半直線BQ'上に点Qを∠AQB < ∠AQ'B = ∠APBとなるように置きます。

∠AQB < ∠AQ'Bなので、

BQ > BQ'
つまり、
点Qは円$O$の外側に存在する
ことになります。

∠AQB > ∠APBの場合

半直線BQ'上に点Qを∠AQB > ∠AQ'B = ∠APBとなるように置きます。

∠AQB > ∠AQ'Bなので、

BQ < BQ'
つまり、
点Qは円$O$の内側に存在する
ことになります。

∠AQB = ∠APBの場合

半直線BQ'上に点Qを∠AQB = ∠AQ'B = ∠APBとなるように置きます。

∠AQB = ∠AQ'Bなので、

BQ = BQ'
つまり、
点Qは点Q'に一致し、円$O$の円周上にに存在する
ことになります。

以上より、

∠AQB = ∠APBならば4点A, B, P, Qは同一円周上に存在する
ことが証明されました。