2024年東北大理系第4問その2

$xyz$ 空間において、点 $\mathrm{P}_1 (3,-1,1)$ を中心とし半径が $\sqrt{5}$ の球面 $S_1$ と、点 $\mathrm{P}_2 (5, 0,-1)$ を中心とし半径が $\sqrt{2}$ の球面 $S_2$ を考える。
(1) 線分 $\mathrm{P_1 P_2}$ の長さを求めよ。
(2) $S_1$ と $S_2$ が交わりをもつことを示せ。この交わりは円となる。この円を $C$ とし、その中心を $\mathrm{P}_3$ とする。 $C$ の半径および中心 $\mathrm{P}_3$ の座標を求めよ。
(3) (2)の円 $C$ に対し、を含む平面を $H$ とする。 $xy$ 平面と $H$ の両方に平行で、大きさが1のベクレルをすべて求めよ。
(4) 点Qが(2)の円 $C$ 上を動くとき、Qと $xy$ 平面の距離 $d$ の最大値を求めよ。また、 $d$ の最大値を与える点Qの座標を求めよ。

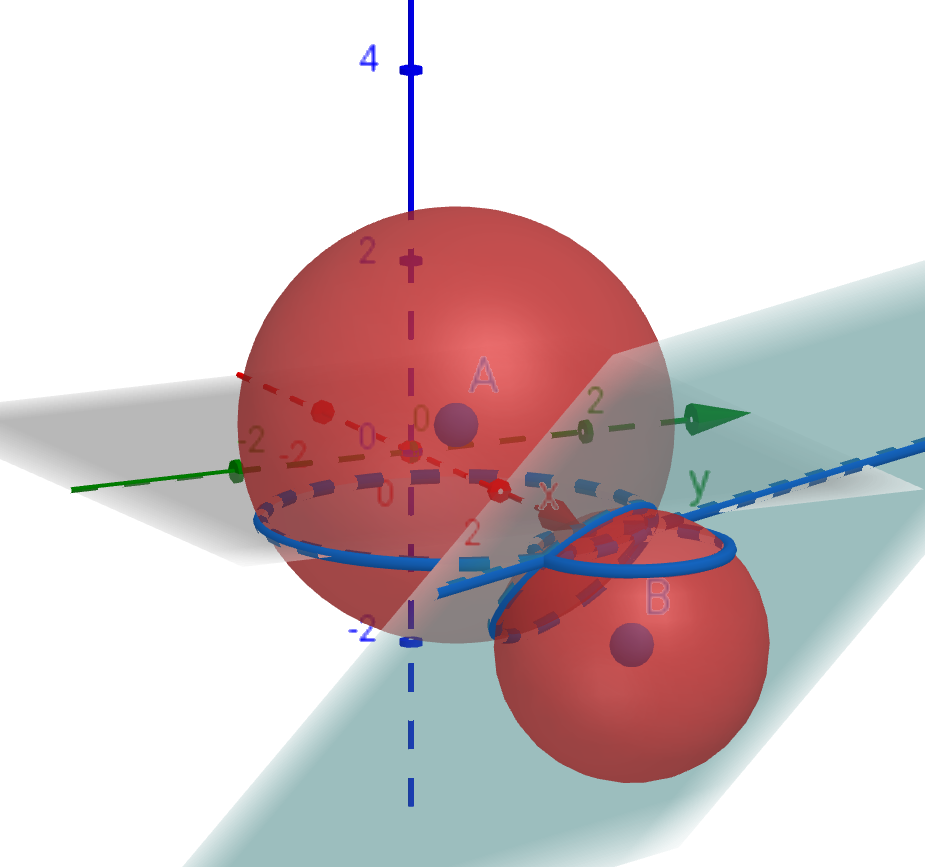
小問(1)の解答例
小問(2)の解答例
小問(3)の解答例
小問(4)の解答例
解説

小問(1)の解答例

小問(2)の解答例

2024年東北大理系第4問その1 - 数式で独楽する

小問(3)の解答例

まず、平面 $H$ を表す式を求めていきます。
球面 $S_1, S_2$ を表す式はそれぞれ
\begin{eqnarray}
S_1 &:& (x -3)^2 +(y +1)^2 +(z -1)^2 = 5 \\
S_2 &:& (x -3)^2 +y^2 +(z +1)^2 = 2
\end{eqnarray}です。円 $C$ 上の点Q $(\xi, \eta, \zeta)$ は $S_1, S_2$ 上にあるので、
\begin{eqnarray}
(\xi -3)^2 +(\eta +1)^2 +(\zeta -1)^2 &=& 5 \\
(\xi -5)^2 +\eta^2 +(\zeta +1)^2 &=& 2
\end{eqnarray}を共に満たします。
この2つの式を展開します。
\begin{eqnarray}
\xi^2 -6\xi +9^2 +\eta^2 +2\eta +1 +\zeta^2 -2\zeta +1 &=& 5 \\
\xi^2 -10\xi +25 +\eta^2 +\zeta^2 +2\zeta +1 &=& 2
\end{eqnarray}辺々相引き、整理します。
\begin{eqnarray}
4\xi -16 +2\eta +1 -4\zeta &=& 3 \\
4\xi +2\eta -4\zeta &=& 18 \\
2\xi +\eta -2\zeta &=& 9
\end{eqnarray}つまり、平面 $H$ を表す式は
\begin{equation}
2x +y -2z = 9
\end{equation}となります。

該当するベクトルを $\vec{v} = (v_1, v_2, v_3)$ とします。
$\vec{v}$ は $H$ の法線ベクトル(2, 1, -2)と $xy$ 平面( $z = 0$ )の法線ベクトル(0, 0, 1)の双方と直交するので、
\begin{eqnarray}
2v_1 +v_2 -2v_3 &=& 0 \\
v_3 &=& 0
\end{eqnarray}が成り立ちます。これより、
\begin{equation}
v_2 = -2v_1
\end{equation}となります。
大きさが1なので
\begin{equation}
{v_1}^2 +{v_2}^2 = 5{v_1}^2 = 1
\end{equation}です。したがって
\begin{equation}
v_1 = \frac{1}{\sqrt{5}}
\end{equation}を得ます。
よって、求めるベクトルは
\begin{equation}
\vec{v} = \frac{1}{\sqrt{5}} (1, -2, 0)
\end{equation}となります。

小問(4)の解答例

平面 $H$ の法線ベクトル(2, 1, -2)と $\vec{v}$ の双方に垂直なベクトル $\vec{u} = (u_1, u_2, u_3)$ は平面 $H$ に平行、かつ平面 $H$ と $xy$ 平面が共有する直線に垂直になります。
\begin{eqnarray}
2u_1 +u_2 -2u_3 &=& 0 \\
u_1 -2u_2 &=& 0
\end{eqnarray}が成り立つので、
\begin{eqnarray}
u_1 &=& 2u_2 \\
u_3 &=& \frac{5}{2} \, u_2 \\
\vec{u} &=& \frac{u_2}{2} (4,2,5)
\end{eqnarray}となります。
大きさを1とすると
\begin{eqnarray}
\frac{{u_2}^2}{4} \cdot 45 &=& 1 \\
u_2 &=& \frac{2}{3\sqrt{5}} \\
\vec{u} &=& \frac{1}{3\sqrt{5}} (4,2,5)
\end{eqnarray}を得ます。

小問(2)の結果から、
\begin{equation}
\overrightarrow{\mathrm{OQ}} = \overrightarrow{\mathrm{OP_3}} -\vec{u}
\end{equation}となる点Qが、 $xy$ 平面との距離 $d$ が最大となります。
したがって、
\begin{equation}
d_\mathrm{max} = -\frac{1}{3} -\frac{\sqrt{5}}{3}
\end{equation}となります。
このとき、点Qの座標は
\begin{equation}
\left( \frac{13}{3} -\frac{4\sqrt{5}}{15}, \ \frac{1}{3} -\frac{2\sqrt{5}}{15}, \ -\frac{1}{3} -\frac{\sqrt{5}}{3} \right)
\end{equation}です。

解説

法線ベクトルとは、平面に垂直なベクトルです。
法線ベクトルに垂直なベクトルは、平面に平行になります。
小問(3)ではこのことを用いています。
小問(4)では、平面 $H$ と $xy$ 平面が共有する直線に垂直かつ平面 $H$ に平行なベクトルを求めています。これで、 $xy$ 平面から最速で離れていくさまを表現しています。