2024年 東北大 理系 第4問 その1

空間において、点を中心とし半径がの球面と、点を中心とし半径がの球面を考える。

(1) 線分の長さを求めよ。

(2) とが交わりをもつことを示せ。この交わりは円となる。この円をとし、その中心をとする。の半径および中心の座標を求めよ。

(3) (2)の円に対し、を含む平面をとする。平面との両方に平行で、大きさが1のベクレルをすべて求めよ。

(4) 点Qが(2)の円上を動くとき、Qと平面の距離の最大値を求めよ。また、の最大値を与える点Qの座標を求めよ。

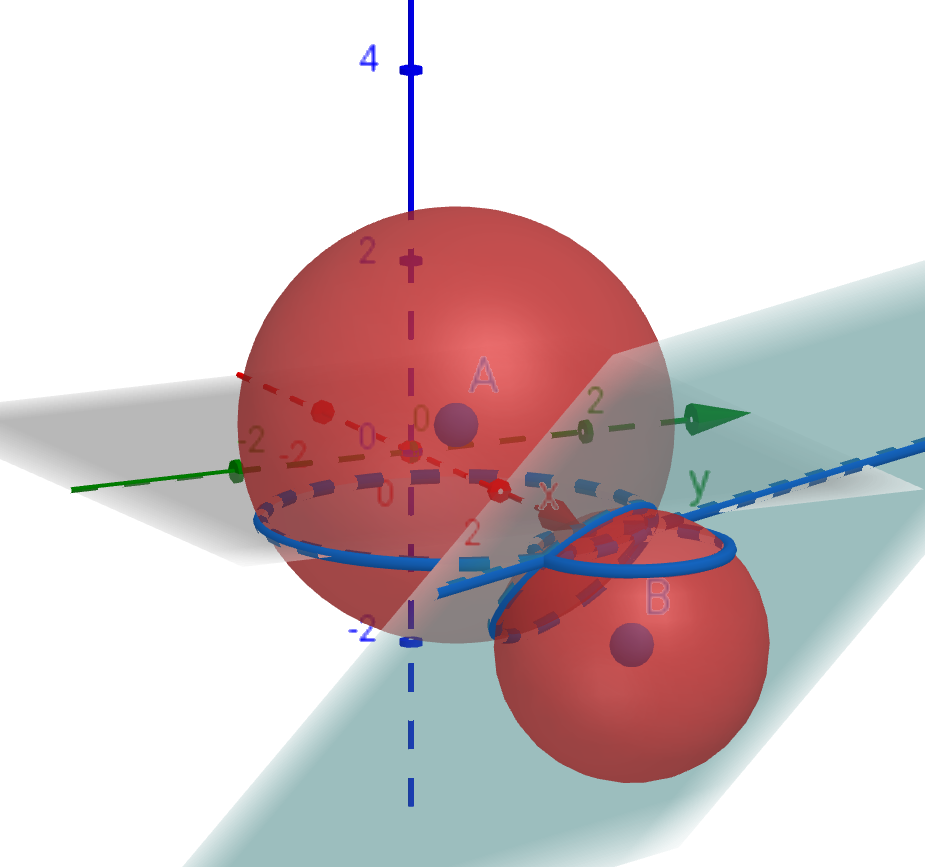
小問(1)の解答例

\begin{eqnarray}
\mathrm{P_1 P_2} &=& \sqrt{(5 -3)^2 +\left \{ 0 -(-1) \right \}^2 +(-1 -1)^2} \\
&=& \sqrt{4 +1 +4} \\
&=& 3
\end{eqnarray}

小問(2)の解答例

(i) の半径をそれぞれとすると、
\begin{eqnarray}
r_1 &=& \sqrt{5} \\
r_2 &=& \sqrt{2}
\end{eqnarray}です。
\begin{equation}
r_1 -r_2 < \mathrm{P_1 P_2} < r_1 +r_2
\end{equation}なので、は交わりを持ちます。(証明終わり)

(ii) の半径をとすると、
\begin{equation}
\sqrt{5 -r^2} +\sqrt{2 -r^2} = 3
\end{equation}が成り立ちます。

\begin{equation}
\sqrt{2 -r^2} = s
\end{equation}とおくと、
\begin{eqnarray}
\sqrt{3 +s^2} &=& 3 -s \\
3 +s^2 &=& 9 -6s + s^2 \\
\therefore \quad s &=& 1
\end{eqnarray}となります。
なので、
\begin{equation}
r = 1
\end{equation}を得ます。

(iii) 上記(ii)の結果より、
\begin{eqnarray}
\mathrm{P_2 P_3} &=& 1 \quad (= s)\\
\mathrm{P_1 P_3} &=& 2
\end{eqnarray}です。

また、
\begin{eqnarray}
\overrightarrow{\mathrm{P_1 P_2}} &=& \left( 5-3, \, 0-(-1), \, -1-1 \right) \\
&=& (2,1,-2)
\end{eqnarray}であることから、小問(1)の結果と合わせて
\begin{eqnarray}
\overrightarrow{\mathrm{OP_3}} &=& \overrightarrow{\mathrm{OP_1}} +\overrightarrow{\mathrm{P_1 P_3}} \\
&=& \overrightarrow{\mathrm{OP_1}} +\frac{2}{3} \, \overrightarrow{\mathrm{P_1 P_2}} \\
&=& (3,1,-1) +\frac{2}{3} (2,1,-2) \\
&=& \left( \frac{13}{3}, \, \frac{1}{3}, \, -\frac{1}{3} \right)
\end{eqnarray}となります。

ゆえに、P₃の座標は、
\begin{equation}
\left( \frac{13}{3}, \, \frac{1}{3}, \, -\frac{1}{3} \right)
\end{equation}です。

小問(3)の解答例

小問(4)の解答例

続きます。
2024年 東北大 理系 第4問 その2 - 数式で独楽する

解説

小問(1)は解説不要です。
小問(2)は3つの部分に分かれています。
第1の部分は、三角形の成立条件を満たせばよいです。
第2の部分は、過程に根号が2つ出ますが適切に置き換えると楽です。
第3の部分は、平面と線分の交点を求める方法もあります。長さとベクトルが分かるので、本文の方法が楽です。