2002年後期京大理系第3問 (自信なし)その1

各面が鋭角三角形からなる四面体ABCDにおいて、辺AB
と辺CDは垂直ではないとする。このとき辺ABを含む平面 $\alpha$ に点C、点Dから下ろした垂線の足をそれぞれC', D'とするとき、4点A, B, C', D'がすべて相異なり、しかも同一円周上にとれることを示せ。

面ABCと面ABDを平面 $\alpha$ に展開します。
それぞれ鋭角三角形なので、C, Dは次の1, 2を共に満たす領域に移されます。

図示すると次の図の明るい青で着色した領域で、境界線は含みません。

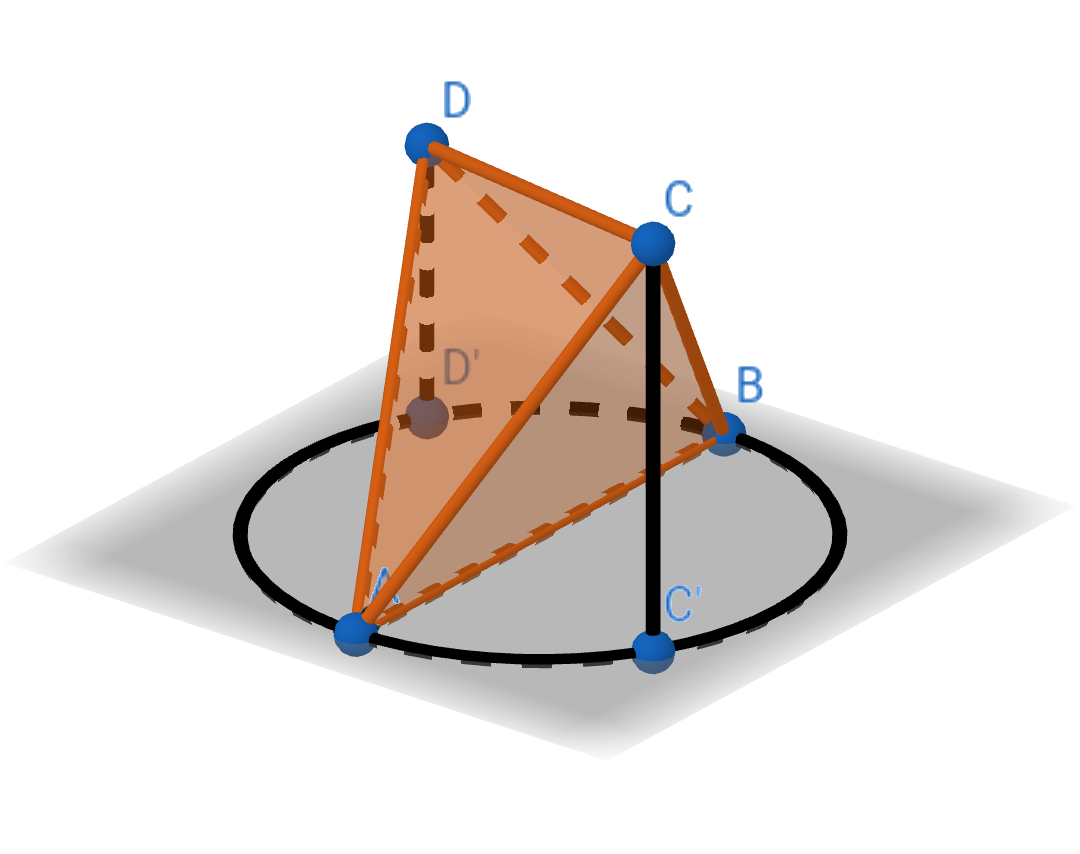
面ABC, ABDを平面 $\alpha$ より起こしていくと、点C', D'が円 $O$ の周上となるように頂点C, Dを置くことができます。

いま、適当な平面 $\alpha$ を定めると、面ABC, ACDを上記の通り展開し、なおかつC', D'が円 $O$ の周上になるように四面体ABCDを復元できます。
よって題意は証明されました。(?)

この解法に自信はありません。
4面全てが鋭角三角形、というのが攻略のカギなのでしょう。
ベクトルで攻めても、鋭角三角形と垂線の足と同一円周上のキーワードが繋がりそうにありませんでした。

なお、この命題より次のことが分かります。
「各面が鋭角三角形からなる四面体は、最も短い辺を直径とする円筒を通過する」