2002年前期京大理系第2問 - 数式で独楽する

半径1の円周上に相異なる3点A, B, Cがある。
(1) $\mathrm{AB^2 +BC^2 +CA^2} > 8$ ならば、△ABCは鋭角三角形であることを示せ。
(2) $\mathrm{AB^2 +BC^2 +CA^2} \leqq 9$ が成立することを示せ。また、この等号が成立するのはどのような場合か。

小問(1)の解答例
小問(2)の解答例
解説

小問(1)の解答例

正弦定理より、
\begin{equation}
\frac{\mathrm{BC}}{\sin A} = \frac{\mathrm{CA}}{\sin B} = \frac{\mathrm{AB}}{\sin C} = 2R = 2
\end{equation}が成り立ちます。
なお、内角の大きさは斜体で表しています。
正弦定理 - 数式で独楽する

△ABCが直角三角形の場合
∠Aを直角としても一般性を失いません。
\begin{eqnarray}
\mathrm{BC} &=& 2 \\
\mathrm{CA} &=& 2\sin B \\
\mathrm{AB} &=& 2\cos B
\end{eqnarray}なので、
\begin{equation}
\mathrm{AB^2 +BC^2 +CA^2} = 4 +4(\sin^2 B +\cos^2 B) =8
\end{equation}となります。

△ABCが鈍角三角形の場合
∠Aを鈍角としても一般性を失いません。
\begin{eqnarray}
\mathrm{BC} &<& 2 \\
\mathrm{CA} &=& 2\sin B \\
\mathrm{AB} &=& 2\sin (A +B) \\
&=& 2\sin (A +B -90^\circ) \\
&<& 2\cos B
\end{eqnarray}なので、
\begin{equation}
\mathrm{AB^2 +BC^2 +CA^2} < 4 +4(\sin^2 B +\cos^2 B) =8
\end{equation}となります。

よって、
\begin{equation}
\mathrm{AB^2 +BC^2 +CA^2} > 8
\end{equation}ならば、△ABCは鋭角三角形であることが示されます。

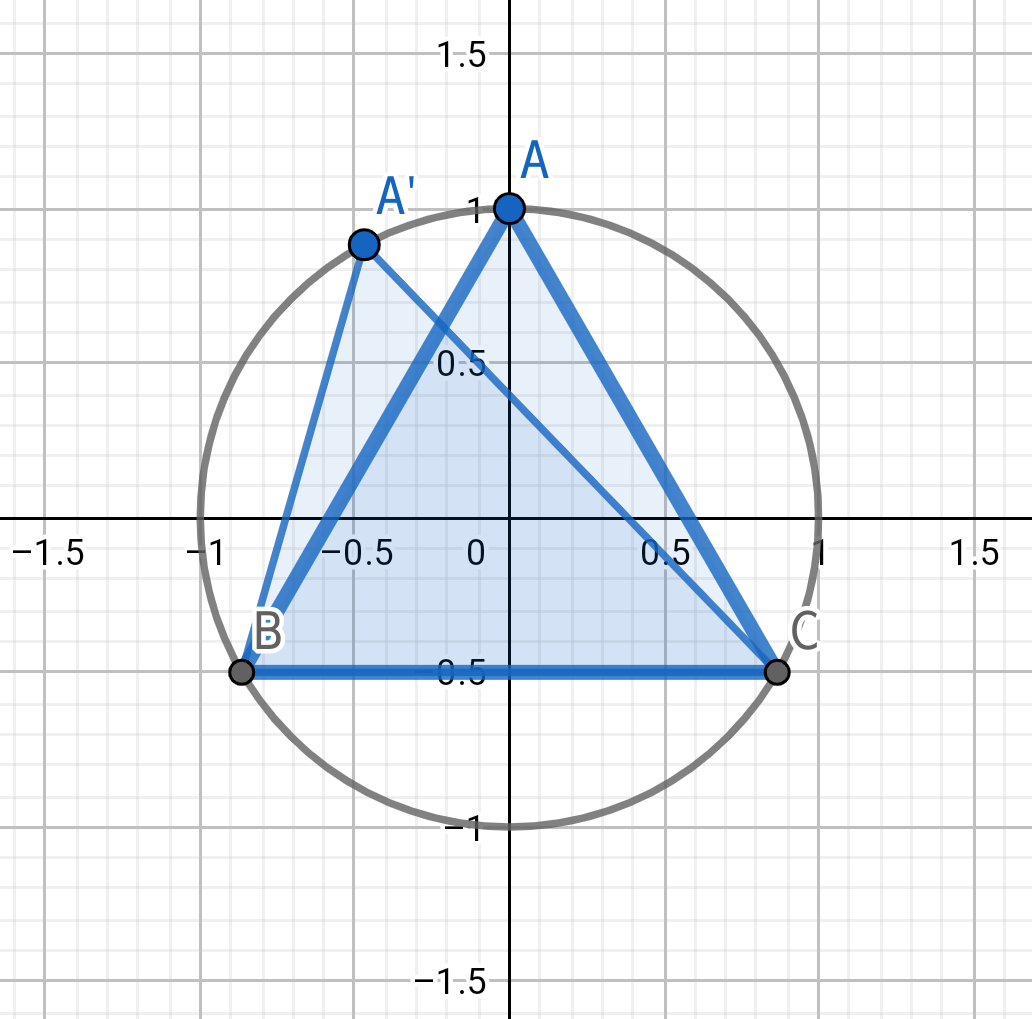
小問(2)の解答例

3点A, B, Cを円 $x^2 +y^2 = 1$ 上に定めます。
また、弦BCを $y = -t \ (0 < t< 1)$ とします。
つまり、
\begin{eqnarray}
\mathrm{A} && (x,y) \\
\mathrm{B} && \left( -\sqrt{1 -t^2}, \ -t \right) \\
\mathrm{C} && \left( \sqrt{1-t^2}, \ -t \right)
\end{eqnarray}とします。

辺BCを固定して頂点Aを動かすと、
\begin{eqnarray}
\mathrm{AB^2 +CA^2} &=& \left( x +\sqrt{1 -t^2} \right)^2 +\left( x -\sqrt{1 -r^2} \right)^2 +2(y +t^2) \\
&=& 2x^2 +2(1 -t^2) +2(y^2 +2ty +t^2) \\
&=& 4(ty +1)
\end{eqnarray}なので、 $y = 1$ 、すなわちA(0, 1)のときに $\mathrm{AB^2 +BC^2 +CA^2}$ は最大となります。

次に、A(0, 1)を固定して辺BCを動かすと、
\begin{eqnarray}
\mathrm{AB^2 +BC^2 +CA^2} &=& 4(1 -t^2) +4(t +1) \\
&=& -4t^2 +4t +8 \\
&=& -4 \left( t -\frac{1}{2} \right)^2 +9 \leqq 9
\end{eqnarray}となります。
よって、題意は証明されました。

等号成立は
\begin{equation}
t = \frac{1}{2}
\end{equation}のときで、このとき、
\begin{equation}
\mathrm{AB^2 = BC^2 = CA^2} =3
\end{equation}つまり△ABCが正三角形となるときです。