京大2021年 理系 第5問

$xy$平面において、2点B, Cに対し、点Aは次の条件(*)を満たす。

(*) かつ 点Aの$y$座標は正

次の各問に答えよ。

(1) △ABCの外心の座標を求めよ。

(2) 点Aが条件(*)を満たしながら動くとき、△ABCの垂心の軌跡を求めよ。

小問(1)の解答例

O(0, 0)とします。
\begin{eqnarray}
\mathrm{OB} = \mathrm{OC} &=& 2 \\
\angle \mathrm{BOC} &=& \frac{2}{3} \pi
\end{eqnarray}です。
条件(*)と円周角の定理の逆により、
点Aは中心O、半径2の円周
\begin{equation}
x^2 +y^2 =4 \tag{1.1}
\end{equation}のの部分を動くことになります。*1
円周角の定理の逆 - 数式で独楽する

この円は△ABCの外接円なので、外心の座標は(0, 0)となります。

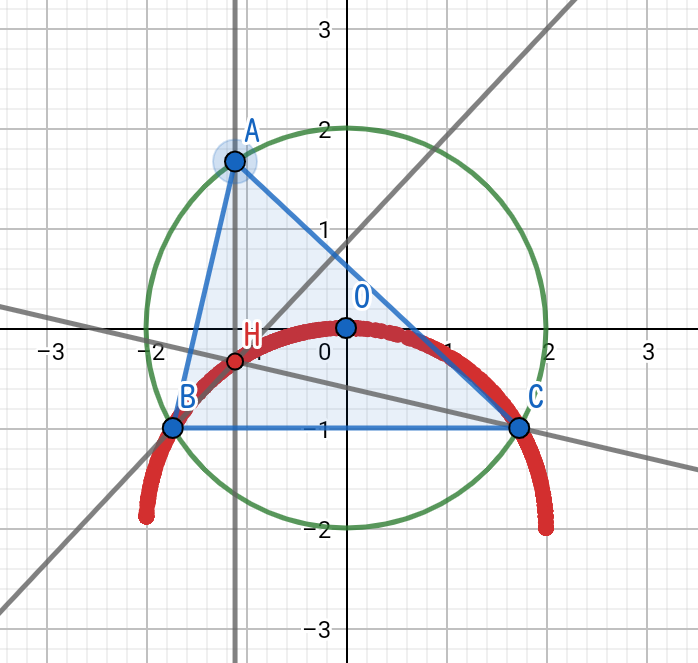
小問(2)の解答例

点Aの座標をとすると、式(1.1)により、
\begin{equation}
s^2 +t^2 = 4 \quad (t > 0) \tag{2.1}
\end{equation}が成り立ちます。

垂心をHとすると、
\begin{eqnarray}
\overrightarrow{\mathrm{CA}} &=& (s -\sqrt{3}, \, t +1) \\
\overrightarrow{\mathrm{BC}} &=& (2 \sqrt{3}, \, 0) \\
\overrightarrow{\mathrm{AH}} &=& (x -s, \, y -t) \\
\overrightarrow{\mathrm{BH}} &=& (x +\sqrt{3}, \, y +1)
\end{eqnarray}です。

より、
\begin{equation}
x = s \tag{2.2}
\end{equation}が成り立ちます。
より、
\begin{equation}
(x +\sqrt{3})(s -\sqrt{3}) + (y +1)(t +1) =0
\end{equation}が成り立ちます。
式(2.2)を用いると、
\begin{equation}
s^2 -3 +(y +1)(t +1) =0
\end{equation}となります。
さらに式(2.1)を用いると、
\begin{eqnarray}
1 -t^2 +(y +1)(t +1) &=& 0 \\
(y +1)(t +1) &=& (t +1)(t -1)
\end{eqnarray}となります。
ここでなので、
\begin{eqnarray}
y +1 &=& t -1 \\
y &=& t -2 > -2 \tag{2.3}
\end{eqnarray}を得ます。

式(2.1)~(2.3)をまとめると、垂心Hの軌跡は、
\begin{equation}
x^2 + (y +2)^2 = 4 \quad (y > -2)
\end{equation}となります。

解説

点Aの座標を未知数とし、角A=60°であることを利用して、第2余弦定理を用いていけば式(1.1)は得られるのでしょう。
中学レベルの幾何を使うとアプローチが楽になる場合があり、本問もそのタイプです。
垂心の方は、座標を未知数として垂線と辺が直交することを代数で表現するのが楽です。

*1:∠BAC=60°の条件だけだと、 \begin{equation} x^2 + y^2 =4 \end{equation}のBCより上の部分と \begin{equation} x^2 +(y +2)^2 =4 \end{equation}のBCより下の部分となります。 もう１つの条件があるので、本文のようになります。