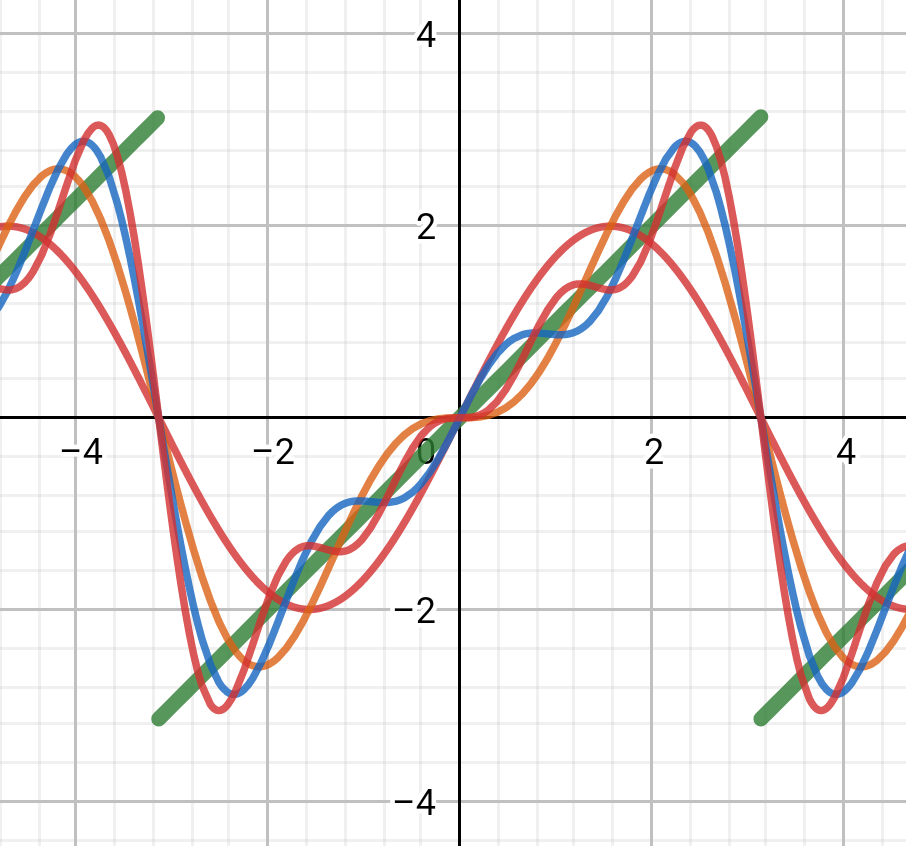
本稿では、鋸歯状波(のこぎり波)のフーリエ級数を見ていきます。
鋸歯状波とは、その名の通り、鋸の歯の形をした波のことです。
波高が徐々に高くなり、急降下するものです。
数式で書くと、次のようになります。
\begin{eqnarray}
f(x) &=& x \quad (-\pi < x < \pi) \\
f(x +2\pi) &=& f(x)
\end{eqnarray}*1

フーリエ級数に展開すると、次のようになります。
\begin{equation}
f(x) = \sum_{n=1}^\infty (-1)^{n -1} \, \frac{2}{n} \, \sin nx
\end{equation}
関数は奇関数なので、奇関数である正弦関数で展開することになります。
フーリエ係数は、
\begin{eqnarray}
b_n &=& \frac{1}{\pi} \int_{-\pi}^\pi x \sin nx \, dx \\
&=& \frac{1}{\pi} \left \{ \left[ -\frac{1}{n} \, x \cos nx \right]_{-\pi}^\pi +\frac{1}{n} \int_{-\pi}^\pi \cos nx \, dx \right \} \\
&=& \frac{1}{\pi} \left \{ (-1)^{n -1} \, \frac{2\pi}{n} +0 \right \} \\
&=& (-1)^{n -1} \, \frac{2}{n}
\end{eqnarray}となります。
フーリエ級数 - 数式で独楽する
なお、2行目の第1項の遷移は、
が奇数の場合
\begin{equation}
-\frac{1}{n} \, \pi (-1) +\frac{1}{n} (-\pi) (-1) = \frac{2\pi}{n}
\end{equation}
が偶数の場合
\begin{equation}
-\frac{1}{n} \, \pi +\frac{1}{n} (-\pi) = -\frac{2\pi}{n}
\end{equation}です。
よって、
\begin{equation}
f(x) = \sum_{n=1}^\infty (-1)^{n -1} \, \frac{2}{n} \, \sin nx
\end{equation}となります。