円周率は、次のように表すことができます。
\begin{eqnarray}
\frac{\pi}{4} &=& 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots \\
\frac{\pi}{4} &=& \sum_{n=0}^{\infty} \frac{(-1)^n}{2n + 1}
\end{eqnarray}
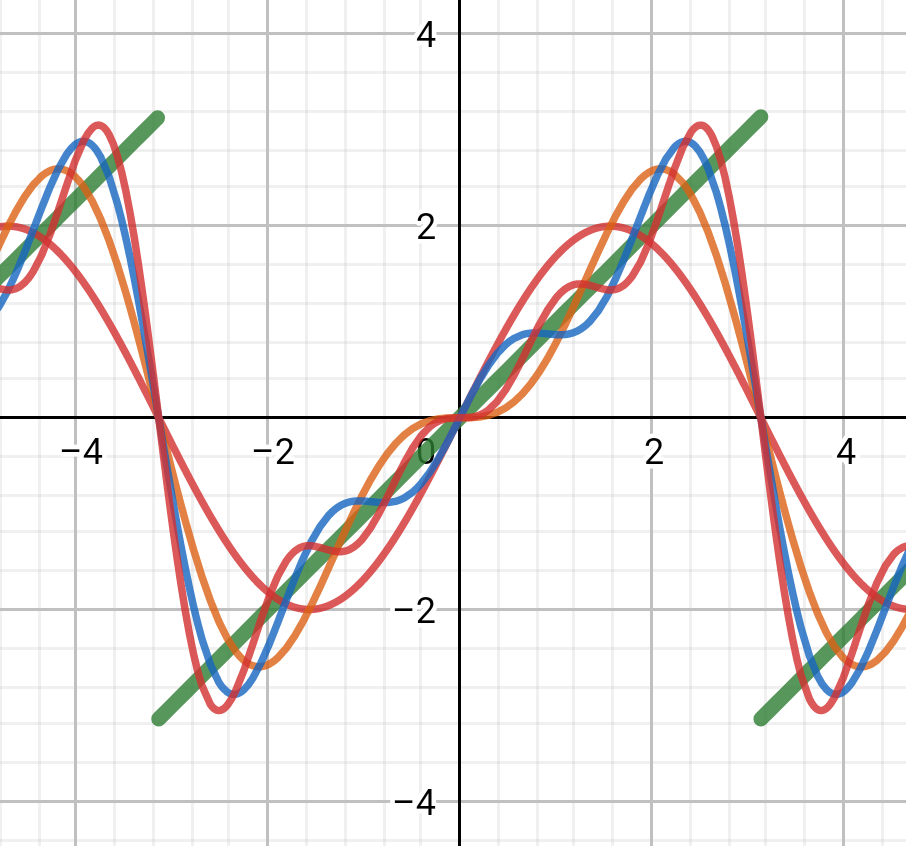
この関係は、鋸歯状波のフーリエ級数展開から導くこともできます。
\begin{eqnarray}
f(x) &=& x \quad (-\pi < x < \pi) \\
f(x +2\pi) &=& f(x)
\end{eqnarray}のとき、
\begin{equation}
f(x) = \sum_{n=1}^\infty (-1)^{n -1} \, \frac{2}{n} \, \sin nx
\end{equation}
鋸歯状波のフーリエ級数 - 数式で独楽する
のみに着目すると、
\begin{equation}
x = \sum_{n=1}^\infty (-1)^{n -1} \, \frac{2}{n} \, \sin nx
\end{equation}となります。
この式にを代入します。
\begin{equation}
\frac{\pi}{2} = \sum_{n=1}^\infty (-1)^{n -1} \, \frac{2}{n} \, \sin \frac{n \pi}{2}
\end{equation}
の場合、
\begin{equation}
\sin \frac{n \pi}{2} = \sin k \pi = 0
\end{equation}です。
の場合、
\begin{equation}
\sin \frac{n \pi}{2} = \sin \frac{(2k +1)\pi}{2} = (-1)^k
\end{equation}です。
\begin{equation}
(-1)^{n -1} = (-1)^{2k} =1
\end{equation}を踏まえると、
\begin{equation}
\frac{\pi}{2} = \sum_{k =0}^\infty (-1)^k \, \frac{2}{2k +1}
\end{equation}を得ます。
以上より、
\begin{eqnarray}
\frac{\pi}{4} &=& \sum_{k =0}^\infty \frac{(-1)^k}{2k +1} \\
\frac{\pi}{4} &=& 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots
\end{eqnarray}を得ます。