サイクロイドの長さ - 数式で独楽する

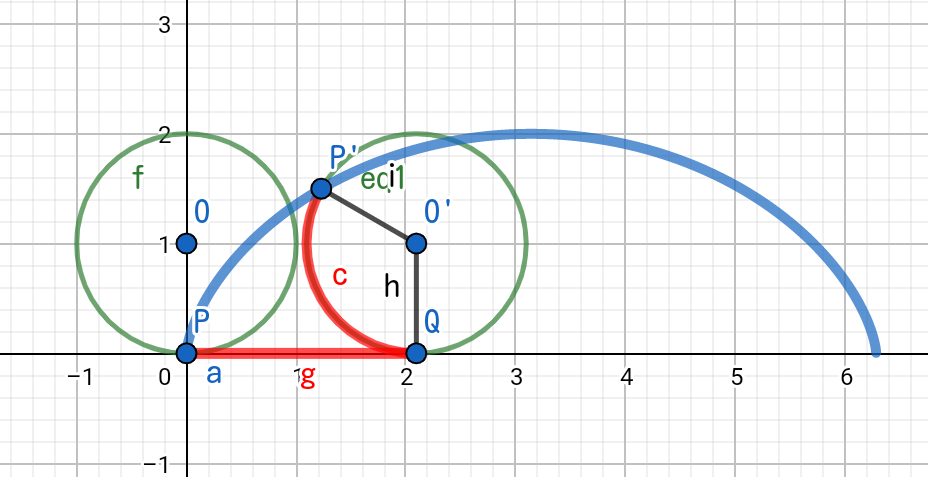
直線上を円が転がるとき、円上の点が描く軌跡を「サイクロイド」といいます。

半径 $a$ の円 $x^2 + (y -a)^2 = a^2$ が $x$ 軸上を右へ転がるとき、原点にあった点Pの軌跡は、
\begin{eqnarray}
x &=& a(\theta - \sin \theta) \\
y &=& a(1- \cos \theta)
\end{eqnarray}と書くことができます。
変換 $x,y$ は別の変数 $\theta$ で表されています。こういう $\theta$ のような変数を、媒介変数といいます。
サイクロイド - 数式で独楽する

サイクロイドの長さ $l$ は
\begin{equation}
l = 8a
\end{equation}です。

導出していきましょう。

曲線の長さは
\begin{equation}
l = \int_0^{2\pi} \sqrt{ \left( \frac{dx}{d\theta} \right)^2 + \left( \frac{dy}{d\theta} \right)^2} \, d\theta
\end{equation}です。
曲線の長さ - 数式で独楽する

\begin{eqnarray}
\frac{dx}{d\theta} &=& a(1 - \cos \theta) \\
\frac{dy}{d\theta} &=& a \sin \theta
\end{eqnarray}なので、
\begin{eqnarray}
\left( \frac{dx}{d\theta} \right)^2 + \left( \frac{dy}{d\theta} \right)^2
&=& a^2 (1 -\cos \theta)^2 + a^2 \sin^2 \theta \\
&=& a^2 (1 -2\cos \theta +\cos^2 \theta + \sin^2 \theta) \\
&=& 2a^2 (1 -\cos \theta) \\
&=& 4a^2 \sin^2 \frac{\theta}{2}
\end{eqnarray}となります。
式変形の最後は半角の公式です。
半角の公式 - 数式で独楽する

したがって、
\begin{equation}
l = 2a \int_0^{2\pi} \left| \sin \frac{\theta}{2} \right| d\theta
\end{equation}となります。2乗に平方根がかかっているので、平方根を外して絶対値記号を被せています。

$0 \leqq \theta \leqq 2\pi$ は $0 \leqq \displaystyle \frac{\theta}{2} \leqq \pi$ なので、
\begin{equation}
\sin \frac{\theta}{2} \geqq 0
\end{equation}です。

よって、
\begin{eqnarray}
l &=& 2a \int_0^{2\pi} \sin \frac{\theta}{2} \, d\theta \\
&=& 2a \left[ -2 \cos \frac{\theta}{2} \right]_0^{2\pi} \\
&=& 4a \Bigl[ -(-1) +1 \Bigr] \\
&=& 8a
\end{eqnarray}を得ます。