サイクロイドの面積 - 数式で独楽する

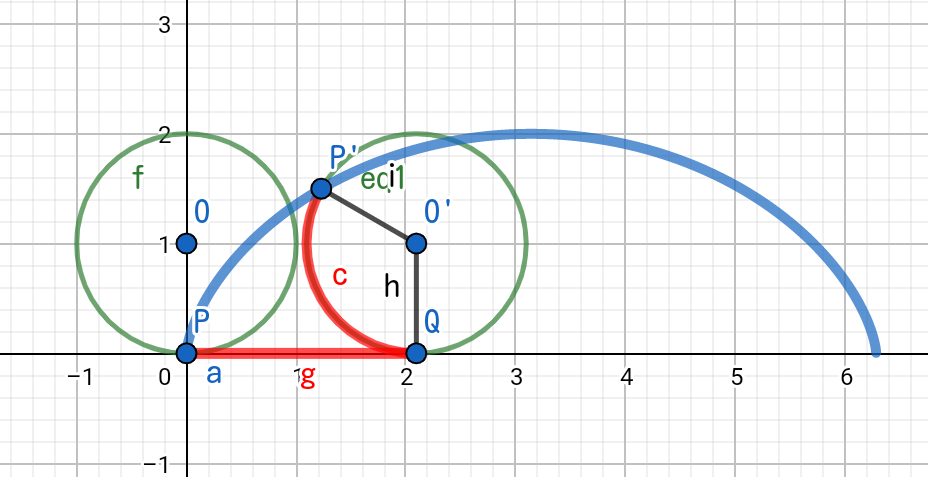
直線上を円が転がるとき、円上の点が描く軌跡を「サイクロイド」といいます。

半径 $a$ の円 $x^2 + (y -a)^2 = a^2$ が $x$ 軸上を右へ転がるとき、原点にあった点Pの軌跡は、
\begin{eqnarray}
x &=& a(\theta - \sin \theta) \\
y &=& a(1- \cos \theta)
\end{eqnarray}と書くことができます。
変換 $x,y$ は別の変数 $\theta$ で表されています。こういう $\theta$ のような変数を、媒介変数といいます。
サイクロイド - 数式で独楽する

サイクロイドと $x$ 軸に囲まれた部分の面積 $S$ は
\begin{equation}
S = 3\pi a^2
\end{equation}です。

みていきましょう。

曲線と $x$ 軸に囲まれた部分の面積は、
\begin{equation}
S = \int_0^{2 \pi a} y \, dx
\end{equation}です。
変数 $x,y$ を媒介変数 $\theta$ を用いて変換します。
\begin{equation}
dx = \frac{dx}{d \theta} \, d \theta = a(1 -\cos \theta) \, d \theta
\end{equation}なので、
\begin{eqnarray}
S &=& \int_0^{2\pi} a^2 (1 -\cos \theta)^2 d\theta \\
&=& a^2 \int_0^{2\pi} (1 -2\cos \theta +\cos^2 \theta) \, d\theta \\
&=& a^2 \int_0^{2\pi} \left( 1 -2\cos \theta + \frac{1 + \cos 2\theta}{2} \right) \, d\theta \\
&=& a^2 \cdot \frac{3}{2} \cdot 2\pi \\
&=& 3\pi a^2
\end{eqnarray}を得ます。